Pattern Matching to Monoids
In the pattern matching process, there are often cases where we want to create patterns that will match against objects with differing numbers of parameters. Examples include wanting to match against the first parameter of any object that has parameters or matching to any Add object that contains a parameter that has a particular pattern (like "a/b", for example).
In order to be able to express this kind of pattern match, we introduce an object named ListVariable in the Code namespace. ListVariable is typed as U -> U where “U” is a type variable, and if the parameter of the ListVariable object is “a”, then it’s normally rendered as “a…”.
The ListVariable object is designed to allow us to express various ways of pattern matching against lists. A list here refers to any object that has a type definition of the form:
TypeA[] -> TypeB
So a simple example would be to create a pattern to pick off the first parameter of an Add object independent of how many parameters the Add object contains. The pattern we use in this case would be:
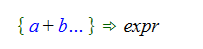
List variables are most commonly used for matching when the parent object (Add in this case) is a monoid. Matching against a monoid is straightforward in this case because if we start with Add[x, y, z, w] we can use the monoid property of Add to write this as Add[x, Add[y, z, w]]. Now we can do the pattern match directly and we bind the variable “a” to “x” and “b” to Add[y, z, w].
A bit more complicated example would be to match against terms in an Add object that have the form b/c. The pattern we want in this case uses two list variables:
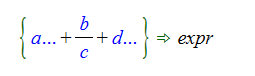
If we the expression we are matching to is Add[x, y/z, u, w] then it’s clear that we want to rewrite this as Add[x, y/z, Add[u, w]] and the bindings are:
- a = x
- b = y
- c = z
- d = Add[u, w]
But the process of finding this match has several steps. The pattern matcher will test each possible combination of parameters in the “a” and “d” list variables as it tries to find a parameter that matches the b/c pattern. If the pattern is:
{ a... + b + c... }
then there four sets of bindings that can be generated by the pattern matching when this pattern is matched to the expression x + y + z + w. The matches are: { a = Add[], b = x, c = y + z + w }, { a = x, b =y, c = z + w }, { a = x + y, b = z, c = w } and { a = x + y + z, b = w, c = Add[] }. For each set of bindings, a + b + c returns the original expression when "a", "b" and "c" are replaced with the bound values.
Note that the pattern matching process in this last example is capable of generating more than one match for some target expressions. For example, if the expression being matched is x + y/z + y/w + u, then there are two possible matches. The pattern matching process will generate both matches and the details of the processing when this pattern match is used in an Assert clause are described in the section on Clauses.
To this point, we have only used list variables in patterns where the parent object is a monoid because it’s only in this case that we can rewrite the expression we are matching against so that we can bind to the parameters of the pattern. As an example, if we have an object f(x, y, z) where “f” is not a monoid, then we can’t rewrite it as f(x, f(y,z)) and the match against a pattern like f[a, b…] doesn’t appear to work.
But there is a way to extend the pattern matching so that these kinds of patterns can be used. In particular, there are cases where we want to write a pattern like g[a, b…] where “g” is a variable and the intent would be to pattern match against any expression that has at least one parameter.
To get this pattern match to work, we introduce the ParameterList object. This object is typed as [U] -> U, where “U” is a variable and is defined to be a monoid. Now, before we do the pattern match we just map the parameters of the expression we will match against into the parameter list object and then pattern match against that. So basically, we just take f(x, y, z) which is the expression we want to match against and rename it to be ParameterList[x, y, z]. Now we can rewrite as ParameterList[x, ParameterList[y, z]] and the bindings against the pattern g[a, b…] are:
- g = f
- a = x
- b = ParameterList[y, z]
Note that the “b” variable in list variable binds to a ParameterList object.
We can also reverse this process and put a ParameterList object back into a function like “f”.
Common patterns involving list variables
There are several patterns involving list variables that are commonly used. We list a few of them here.
The first patterns are patterns containing one list variable, for example:
{ a… + b }
{ a + b… }
these patterns are commonly used in recursive processing to pick off either the first or last item from a list, do something to it and then process the rest of the list.
Patterns containing two list variables
{ a… + b + c… }
Matching any pair of parameters
{ a… + b + c… + d + e… }
In general, it would be unusual to create a pattern that had two list variables in a row. Although
{ a... + b... }
is valid, it's not clear what it would be used for. If there is more than one list variable in a pattern, there is almost always something else in between.
Patterns with list variables when the expression is not a monoid
Patterns with list variables can also be used to match against expressions where the parent term is not a monoid. For example, there is a PropertiesList object that typed as [Property] → PropertyList. If we want to search for a particular property in a property list, we would want a pattern match something like:
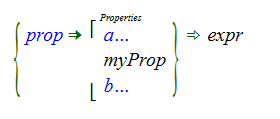
but the question would be, what are the expressions bound to the variables "a" and "b"? If "a" and "b" were PropertyList objects, then it wouldn't be the case that we could reconstruct the original expression by building the expression PropertyList[a, myProp, b].
Instead, we need the "a" and "b" parameters to be bound to ParameterList objects. If we take this approach, the expression PropertyList[a, myProp, b] will build back to the original expression. See The ParameterList Object for more details.
Binding to a ParameterList when the expression is a monoid
There are occasions when we need to extract some or all of the parameters of a monoid and put those parameters into another object. For example, suppose you wanted to take some of the parameters of a List object and put them into a Set object. Suppose the List contains integers and that we know that the integers are ordered. To extract the elements of the list greater than 10 and less than 100, we could try:
{ a => List[ b..., 10, c..., 100, d...] } => Set[c]
but that gives Set[List[…]], which is not what we want.
We can get the expression we want if "c" is bound to a ParameterList object and we can accomplish that using the ListVariableParamList object in the pattern.
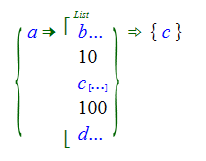
Because we aren't using "b" and "d" here, it doesn't matter whether we bind them using a ListVariable object or a ListVariableParamList object.