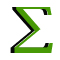Conditions in Type Definitions

Conditions in type definitions are used to further restrict the types that are valid for a type variable in a type definition. A type definition with conditions might look like Type: U → U with (condition)

The expression that appears after the "with:" in a type definition that has conditions can be either a single condition

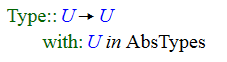
or it can be a list of conditions

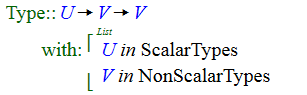
There are three expressions that are valid conditions. A condition can be an equality, it can be a subtype statement or it can be a statement like the ones shown here that uses the In object.

Equality conditions

An equality condition has the form

U = (expression)

where the left-hand side (U in the example) must be a type variable that appears in the type definition.

An equality condition like U = Real is allowed, but doesn't really serve any purpose since it's equivalent to just putting Real directly into the type definition.

The right-hand side of an equality condition can contain any expression that is valid in the type definition itself and it can also contain TypeUnion and/or TypeIntersection terms.

For example, you could create a type definition like

U → V → W with W = Set[TypeUnion[U, V]]

Subtype conditions

A subtype condition has the form

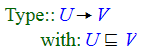
Typically, either the left-hand side or the right-hand side is just a type variable that appears in the type definition, but more complicated expressions are valid.

In conditions

These conditions have the form

U in Types

where the left-hand side (U in the example) must be a type variable that appears in the type definition or the ResultType of a type variable the appears in the type definition

This type definition condition is used to restrict a variable in a type definition to be one of the types in the list of types specified on the right-hand side of the condition. There are two ways to do this. The first is to list the types explicitly in the condition - for example:

The second way to do this is for the condition to specify the name of a function that returns a list of types - for example:

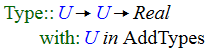
In this case, the Sym type inferencer will call the function to retrieve the list of types.

The second approach has the advantage that it's possible to extend the list of types that are included in a type definition when new libraries are created by adding the additional types as an extension to the function.

The ResultType Object

Conditions can also contain the ResultType object. The ResultType object lets you apply a condition only to the result type of an object. For example, with this type definition

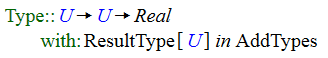
U can not only be one of the types in AddTypes, but it can be any map to one of the types in AddTypes. If AddTypes includes the Real type, then a type like TypeA → Real and TypeA → TypeB → Real, and so on, are all valid types for the type variable U.

Using the ResultType object allows you, for example, to include operator types in the set of valid types for the Add object.